Newton And Leibniz: The Fathers Of Calculus

Calculus is commonly accepted to have been created twice, independently, by two of the seventeenth century’s brightest minds: Sir Isaac Newton of gravitational fame, and the philosopher and mathematician Gottfried Leibniz. The consensus has not always been so peaceful, however: the late 1600s saw fierce debate between the two thinkers, with each claiming the other had stolen his work.

So, what really is calculus, and how did it become such a contested field?

What is calculus?

Simply put, calculus is the study of continuous change. It was originally called the calculus of infinitesimals, as it uses collections of infinitely small points to consider how variables change.

Differentiation and integration are the main concerns of the subject, with the former focusing on instant rates of change and the latter describing the growth of quantities. This means differentiation looks at things like the slope of a curve, while integration is concerned with the area under or between curves. Calculus discusses how the two are related, and its fundamental theorem states that they are the inverse of one another. This unification of differentiation and integration, paired with the development of notation, is the focus of calculus today.

Need help preparing for college or university? Master advanced topics like Calculus and Algebra with expert tutors at our Online Summer Courses and Oxford Summer School.

The origin of calculus

Let’s journey through history to uncover the origins and evolution of calculus.

Ancient times

Like many areas of mathematics, the basis of calculus has existed for millennia. Democritus worked with ideas based upon infinitesimals in the Ancient Greek period, around the fifth century BC. The Greeks would only consider a theorem true, however, if it was possible to support it with geometric proof. Greek philosophers also saw ideas based upon infinitesimals as paradoxes, as it will always be possible to divide an amount again no matter how small it gets.

At some point in the third century BC, Archimedes built on the work of others to develop the method of exhaustion, which he used to calculate the area of circles. This is similar to the methods of integrals we use today.

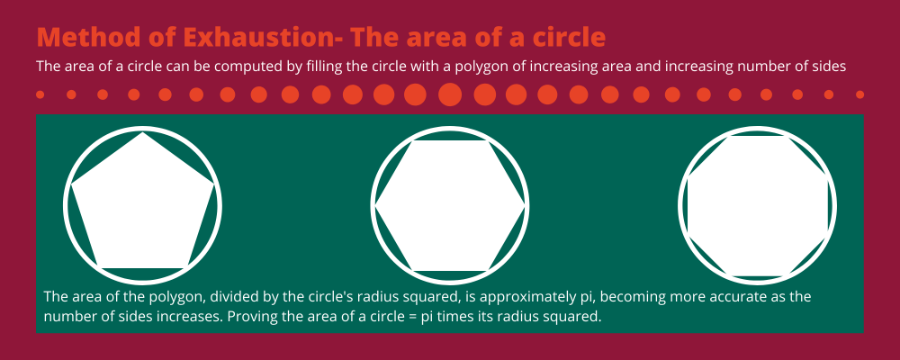
After the ancient Greeks, investigation into ideas that would later become calculus took a bit of a lull in the western world for several decades.

The Middle East and India

As with many other areas of scientific and mathematical thought, the development of calculus stagnated in the western world throughout the Middle Ages.

Meanwhile, on the other side of the world, both integrals and derivatives were being discovered and investigated. An Arab mathematician, Ibn al-Haytham was able to use formulas he derived to calculate the volume of a paraboloid – a solid made by rotating part of a parabola (curve) around an axis.

There was an apparent transfer of ideas between the Middle East and India during this period, as some of these ideas appeared in the Kerala School of Astronomy and Mathematics. While many of calculus’ constituent parts existed by the beginning of the fourteenth century, differentiation and integration were not yet linked as one study.

The fourteenth century

Back in the western world, a fourteenth century revival of mathematical study was led by a group known as the Oxford Calculators. A collection of scholars mainly from Merton College, Oxford, they approached philosophical problems through the lens of mathematics. The Merton Mean Speed Theorem, proposed by the group and proven by French mathematician Nicole Oresme, is their most famous legacy. It concerns speed, acceleration and distance, and arguably revived interest in the study of motion.

The seventeenth century

Arguably the most transformative period in the history of calculus, the early seventeenth century saw René Descartes’ invention of analytical geometry, and Pierre de Fermat’s work on the maxima, minima and tangents of curves. Some of Fermat’s formulas are almost identical to those used today, almost 400 years later.

Fermat also contributed to studies on integration, and discovered a formula for computing positive exponents, but Bonaventura Cavalieri was the first to publish it in 1639 and 1647. Blaise Pascal integrated trigonometric functions into these theories, and came up with something akin to our modern formula of integration by parts. A whole host of other scholars were also working on theories which contributed to what we now know as calculus in this period, so why are Newton and Leibniz known as the real creators?

The key element scholars were missing was the direct relation between integration and differentiation, and the fact that each is the inverse of the other. Isaac Barrow, Newton’s teacher, was the first to explicitly state this relationship, and offer full proof. However, Newton and Leibniz were the first to provide a systematic method of carrying out operations, complete with set rules and symbolic representation. They were the ones to truly found calculus as we recognise it today. Since they developed their theories independently, however, they used different notation.

The eighteenth century and beyond

The debate surrounding the invention of calculus became more and more heated as time wore on, with Newton’s supporters openly accusing Leibniz of plagiarism. Britain’s insistence that calculus was the discovery of Newton arguably limited the development of British mathematics for an extended period of time, since Newton’s notation is far more difficult than the symbolism developed by Leibniz and used by most of Europe. Today, the universally used symbolism is Leibniz’s.

When studying Newton and Leibniz’s respective manuscripts, it is clear that both mathematicians reached their conclusions independently. While they were probably communicating while working on their theorems, it is evident from early manuscripts that Newton’s work stemmed from studies of differentiation and Leibniz began with integration. They thus reached the same conclusions by working in opposite directions.

Real-life calculus

The study of calculus has been further developed in the centuries since the work of Newton and Leibniz. In the modern day, it is a powerful means of problem-solving, and can be applied in economic, biological and physical studies. It can be applied to the rate at which bacteria multiply, and the motion of a car. Modern physics, engineering and science in general would be unrecognisable without calculus.

Next steps for aspiring mathematicians

• Take a look at this article for more detail on what exactly calculus is.
• Find out more about infinitesimals.
• Find out what it’s like to study math at Oxford university.
• Get an edge in mathematics and other subjects by signing up for one of our Oxford summer courses for teenagers.